Introduction
Queen of Hearts is a silly game played at the Elks in Norwood, Ma. This post originated as an R Markdown file where I simulated the probability of winning during the first week (n=54 cards remain). In this simulation, I assumed 1000 unique participants entered the drawing, each selecting a random number corresponding to where the Queen of Hearts is on the board, randomly from 1 through 54.
```{r, Required R packages} library(tidyverse) library(stringr)
### Methods
First, I made a deck of cards using code that I found somewhere online (sorry random person who deserves credit here).
I set a seed value of 886600 to ensure that every time I come back to run this simulation, I get the same card order when shuffling the deck. The Queen of Hearts is 40th in this shuffle order, [range: 1-54 (deck includes 2 joker cards)].Looking back at this now, I don't think I should set a seed- maybe I will change this and re-run the simulation one day (but I doubt it).
```{r, Making the deck of cards}
#Here I make a deck of cards
set.seed(886600)
buildDeck <- function(noOfDecks=1){
suits <- c("Clubs", "Spades", "Diamonds", "Hearts")
cards <- c("Ace", 2:10, "Jack", "Queen", "King")
Deck <- paste(cards, rep(suits, each = 13), sep = "-")
Deck <- as.data.frame(Deck)
Joker <- c("Joker")
Jokers_In <- as.data.frame(paste(rep(Joker, 2)))
names(Jokers_In) <- "Deck"
Full_Deck <- rbind(Deck, Jokers_In, stringsAsFactors = F)
d <- rep(Full_Deck, noOfDecks) #Build decks
shuffledDeck <- sample(d, length(d)) #Shuffle decks
return(as.data.frame(shuffledDeck))
}
deck <- buildDeck(1)
deck <- deck[sample(1:nrow(deck)),]
deck <- as.data.frame(deck)
queen_of_hearts_number <- 40
deck$og <- 1:54
Next, I made a function that simulated ‘1000 Gregs’ (numbered 1-1000) and randomly assigned each to a card number (1-54).
This represents a real-life scenario in which 1000 people went to the Elks during the first week of the raffle and randomly picked a card number that they thought the Queen of Hearts was ‘hiding.’
Looking back at my younger self, I overlooked one key aspect. This would not apply to scenarios where one person entered multiple guesses during the first week of the content.
For example, if Greg Petrucci Sr. decided he wanted to make two guesses (theoretically doubling his probability of winning), the two numbers he enters are not independent of one another. That is, if his first guess was 11 (because his daughter’s birthday is 11 July), then his second guess (in all likelihood) would be any number other than 11 (i.e. 1-10, 12-54). In this way, the two guesses are not totally random nor independent of the other. Knowing something about his first guess (11) gives some information about his second guess (unless there were some beverages in between the guesses).
```{r, Function for Making the weekly name entry and their respective card number}
#Here I make a function for weekly name entry and column
#2 is the corresponding card number for that participant
weeklyName_Entry <- function(n=1000, dim_deck){
names <- c(rep(“Greg”, n ))
for (i in 1:length(names)){
names[i] <-paste(names[i], i, sep=””)
}
names<- as.data.frame(names)
names$card_number <- NA
for ( i in 1:nrow(names)){
names$card_number[i] <- sample(1:dim_deck, 1)
}
return(names)
}
week_1_names <- weeklyName_Entry(n=1000, dim_deck=54)
Output from above is week1_names, which has 1000 names and random numbers ranging from 1 through nnn.
This represents 1000 unique names entering the drawing in week one, where:
each person chooses a random card number from 1 through nnn.
```{r, Function for testing if the randomly sampled name is same as the criterion name}
summary_results <- data.frame(Name_Binary=rep(NA, 54),
Queen_Binary=rep(NA, 54),
Incorrect_Guess_Number=rep(NA, 54),
Week=rep(NA, 54))
weekly_drawing_for_names_and_queen <- function(week_1_names){
#This function evaluates if the true name is selected
#from the fish bowl, if yes, counter = 0, else counter = 1
for (jjj in 1:nrow(deck)){
if (jjj==1){
week_1_name_winner_index <- sample(1:nrow(week_1_names), 1)
week_1_criterion <- week_1_names[week_1_name_winner_index,]
drawing_winner_index <- sample(nrow(week_1_names), 1)
if (week_1_names[drawing_winner_index,][1,1] == week_1_criterion[1,1]){
#check to see if the name hits
counter_name <- 0
} else {
counter_name <- 1
}
if(week_1_names[drawing_winner_index,][,2]== 40){
#check to see if the queen of hearts numbers hit
counter_queen <- 0
card_incorrect_guess_number <- NA
} else {
counter_queen <-1
card_incorrect_guess_number <- week_1_names[drawing_winner_index,][,2]
}
summary_results[jjj,] <- c(counter_name, counter_queen, card_incorrect_guess_number, jjj)
} else { #end jjj==1 and start week 2 and onwards
if (is.na(card_incorrect_guess_number)==T){
NULL
} else {
deck <- as.data.frame(deck[-card_incorrect_guess_number,])
dim_deck_jjj <- dim(deck)[1]
week_jjj_names <- weeklyName_Entry(n=1000, dim_deck=dim_deck_jjj)
week_jjj_name_winner_index <- sample(1:nrow(week_jjj_names), 1)
week_jjj_criterion <- week_jjj_names[week_jjj_name_winner_index,]
drawing_winner_index <- sample(nrow(week_jjj_names), 1)
drawing_winner_card_length <- as.numeric(week_jjj_names[drawing_winner_index,][2])
drawing_winner_card_og_number <- as.numeric(deck[drawing_winner_card_length,][2])
if (week_jjj_names[drawing_winner_index,][1,1] == week_jjj_criterion[1,1]){
#check to see if the name hits
counter_name <- 0
} else {
counter_name <- 1
}
if(drawing_winner_card_og_number == 40){
#check to see if the queen of hearts numbers hit
counter_queen <- 0
card_incorrect_guess_number <- NA
} else {
counter_queen <-1
card_incorrect_guess_number <- week_jjj_names[drawing_winner_index,][,2]
}
}
summary_results[jjj,] <- c(counter_name, counter_queen, card_incorrect_guess_number, jjj)
}#end else jjj >=2
jjj <- jjj +1
}#end for loop
return(summary_results)
}#end function
```{r, Do simulation studies} number_of_simualtions <- 1000 simulation_resuslts <- data.frame(simualtion=(1:(number_of_simualtions)), week_queen_selected=rep(NA, times=number_of_simualtions), did_dad_name_picked=rep(NA, times=number_of_simualtions), did_dad_win=rep(NA, times=number_of_simualtions) )
for(i in 1:number_of_simualtions){ test <- weekly_drawing_for_names_and_queen(week_1_names) week_queen_selected <- which(is.na(test$Incorrect_Guess_Number))[1] number_of_weeks_not_selected <- sum(test$Name_Binary[1:week_queen_selected], na.rm = T) simulation_resuslts$did_dad_name_picked[i]<-(week_queen_selected-number_of_weeks_not_selected)/(week_queen_selected) simulation_resuslts$week_queen_selected[i] <- week_queen_selected simulation_resuslts$did_dad_win[i] <- any(test$Name_Binary==0 & test$Queen_Binary==0) }#end simulation study for loop
hist(simulation_resuslts$week_queen_selected, breaks=c(53)) unique(simulation_resuslts$did_dad_win) ```
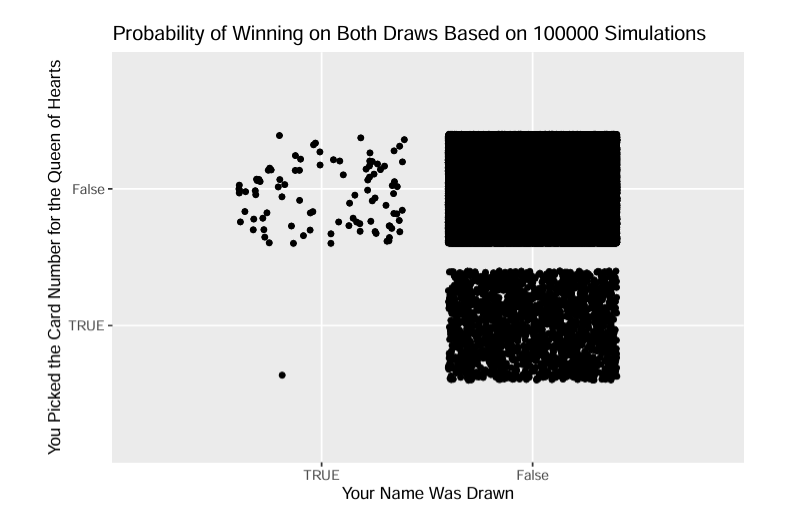
This showed that the queen of hearts was selected on week 38, but Dad did not win, someone else did Questions: 1.) If you do 1000000 simulations, how many times does Dad win? 2.) On average, what week is the queen selected (95% CI)?